Geiger and Marsden performed an experiment in which they have bombarded \alpha-particles on a very thin foil of gold and collected data from the experiment which was later on analysed by Rutherford.
Rutherford explained the data of Geiger and Marsden by making some assumptions.
It was assumed that
- The atom contains a nucleus of charge Ze, where Z is the atomic number of the atom. That is the number of electrons in the neutral atom.
- The nucleus can be treated as a point particle.
- The nucleus is quite massive compared with the mass of the incident \alpha-particle that the nuclear recoil may be neglected.
- The laws of classical mechanics and electromagnetism can be applied and no other forces are present.
- The collision between \alpha-particle and target nucleus is elastic.
For those \alpha-particles which directed towards the centre of the nucleus, the collision between α and the target nucleus is considered as head-on collision and hence the kinetic energy of incident \alpha-particle is equal to the Coulomb energy at nearest approach. If T is the kinetic energy of the incident \alpha-particle and D is the distance of nearest approach, then
\begin{aligned}T&= \dfrac{(2e)(Ze)}{4\pi\epsilon_0 D}\\&= \dfrac{Ze^2}{2\pi\epsilon_0 D}\\ \end{aligned}
And the distance of the nearest approach is calculated as;
D=\dfrac{Ze^2}{2\pi\epsilon_0 T}
The \alpha-particles which directed towards the centre of the nucleus reflected back by 180^0and hence the scattering angle for those \alpha-particles is \theta = 180^0.
Just like the distance of the nearest approach and scattering angle, the impact parameter is also a very important factor here.
The impact parameter is actually the perpendicular distance between the line of incidence of an \alpha-particle and the centre of the nucleus. It is denoted by b.
So, for an \alpha-particles directed towards the centre of the nucleus, the impact parameter is zero.
That is for b = 0, \theta = 180^0
But, if the line of incidence of the \alpha-particle is at a distance from the centre of the nucleus then the scattering angle will be smaller.
And if you want to find the scattering angle of the α at a particular value of an impact parameter then you must have a relation between the scattering angle and an impact parameter.
So, let’s derive a relation between the scattering angle and an impact parameter.
Consider an \alpha-particle approaches the target nucleus in such a way that the line of incidence is at a distance b from the centre of the nucleus as shown in the diagram below.
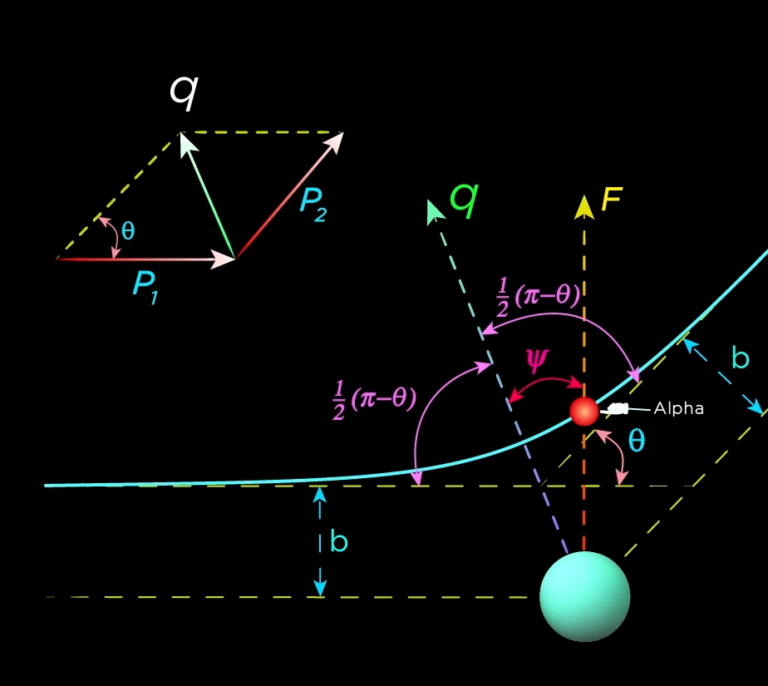
Let;
- the scattering angle of the \alpha-particle is \theta.
- the linear momentum of incident \alpha-particle is \vec{P_1} and
- the linear momentum of the same \alpha-particle after scattering is \vec{P_2}
Now, if we assume that the scattering of the \alpha-particle is elastic then \vec{P_1} and \vec{P_2} will be equal in magnitude and let’s say it is P.
The change in momentum of the \alpha-particle is given by;
\vec{q} =\vec{P_2}-\vec{P_1}
And its direction is along the line joining the nucleus to the point of nearest approach of the \alpha-particle.
From the diagram;
\begin{aligned}|\vec{q}|&=\sqrt{|\vec{P_1}|^2+|\vec{P_2}|^2-|\vec{P_1}||\vec{P_2}|\cos{\theta}}\\&=\sqrt{p^2+p^2-2p^2\cos{\theta}}\\ &=p\sqrt{2(1-\cos{\theta})}\\&=\sqrt{2\times 2\sin^{2}(\frac{\theta}{2})}\\&=2p\sin(\frac{\theta}{2})\\\end{aligned}
If we assume that the nucleus is much heavier than the \alpha-particle then we can neglect its recoil.
Since the speed of \alpha-particles is quite less than the speed of light so we can also neglect any relativistic effects.
If we consider a two-dimensional polar coordinate system in which the centre of the nucleus is taken as the origin, then the coordinates of the position of \alpha-particle is (r, \psi).
Where, \psi = 0 is chosen to be the point of the nearest approach.
By Newton’s second law, the rate of change of momentum in the direction of q is the component of the force acting on the \alpha-particle due to the electric charge of the nucleus.
By Coulomb’s law, the force on the \alpha-particle at (r, \psi) is;
\begin{aligned}F&=\dfrac{(2e)(Ze)}{4\pi\epsilon_0 r^2 }\\&=\dfrac{Ze^2}{2\pi\epsilon_0 r^2 }\\ \end{aligned}
Now we have
\begin{aligned}T&=\dfrac{Ze^2}{2\pi\epsilon_0 D}\\\Rightarrow \dfrac{Ze^2}{2\pi\epsilon_0}&=TD \\ \end{aligned}
so,
F=\dfrac{TD}{r^2}
The component of this force in the direction of q is
F_q =\dfrac{TD}{r^2}\cos\psi
and, therefore, the change of momentum is given by;
\begin{aligned}q&=\int {F_q (t)dt}\\&=\int{\dfrac{TD}{r^2}\cos\psi(t)dt}\\ \end{aligned}
Since, \dot{\psi} =\dfrac{d\psi}{dt} \Rightarrow dt=\dfrac{d\psi}{\psi}
So,
\begin{aligned}q&=\int {\left(\dfrac{TD}{r^2}\cos\psi(t)\times \frac{d\psi}{\psi}\right)}\\ \end{aligned}
Angular momentum of the \alpha-particle before interacting with the nucleus is;
L_1=bp_1=bp
(This is obtained by the relation \vec{L}= \vec{r}\times\vec{P})
Angular momentum of the scattered \alpha-particle at any time t is;
L_2= m_{\alpha} r^2\dot{\psi}
(This is obtained by the relation \vec{L}= I\vec{\omega})
Now from the conservation of angular momentum,
\begin{aligned}L_1 &=L_2\\\Rightarrow bp &=m_{\alpha} r^2 \dot{\psi}\\ \Rightarrow \dot{\psi}&=\dfrac{bp}{ m_{\alpha} r^2 }\\ \end{aligned}
So,
\begin{aligned}q&=\int {\left(\dfrac{TD m_{\alpha} r^2 }{r^2bp}\cos\psi(t)d\psi\right)}\\ \end{aligned}
since
T= \dfrac{P^2}{2 m_{\alpha}}
So,
\begin{aligned}q&=\int {\dfrac{DP }{2b}\cos\psi(t)d\psi}\\ \end{aligned}
From the diagram, \psi varies from -\frac{1}{2} (\pi-\theta) to +\frac{1}{2} (\pi-\theta) so,
\begin{aligned}q&=\int_{-\frac{1}{2} (\pi-\theta)}^{+\frac{1}{2} (\pi-\theta)} {\dfrac{DP }{2b}\cos\psi(t)d\psi}\\ &=\dfrac{DP }{2b}\times 2\sin \left(\frac{1}{2} (\pi-\theta)\right)\\ &=\dfrac{DP }{b}\times \cos \left(\dfrac{\theta}{2}\right)\\ \end{aligned}
We already calculated q= 2p \sin\left(\dfrac{\theta}{2}\right)
So,
\begin{aligned} 2p\sin\left(\dfrac{\theta}{2}\right) &=\dfrac{DP }{b}\times \cos \left(\dfrac{\theta}{2}\right)\\ \Rightarrow \tan \left(\dfrac{\theta}{2}\right) &= \dfrac{D}{2b}\\ \end{aligned}
This is the relation between the scattering angle \theta and impact Parameter b.
