According to the big bang theory, the universe was born around 13.8 billion years ago. After 10^{-6} seconds of the incidence of the Big Bang, neutrons and protons were formed by the combination of quarks and gluons. Then after a few minutes, neutrons combined with protons to form deuterium and helium nuclei and most protons remained uncombined as hydrogen nuclei. And other nuclei were formed quite later than the formation of these three nuclei, hydrogen, deuterium, and helium.
Mass Defect:
After the discovery of the nucleus and its constituents, it was found that the mass of a nucleus is less than the sum of the masses of the constituent protons and neutrons. And the difference between the mass of a nucleus and the sum of the masses of the nucleons of which it is composed is called the mass defect.
Suppose we have a nucleus X and we want to calculate its mass defect. From the definition, the mass defect of the nucleus X is calculated as
\begin{aligned}\text{Mass Defect} &= (Zm_p + (A-Z)m_n – M(A,Z))\\\end{aligned}
where Z is the atomic number of X, A is the mass number of X, M(A,Z) is the mass of the nucleus X and m_p and m_n are the masses of the proton and neutron.
Binding Energy:
Since the nucleus is a bond system so its potential energy is always negative. If nucleons are completely separated, they do not interact and in that case, they have ZERO potential energy.
You can understand it in a different way. Suppose you are trapped at the bottom of a well, you need to climb up the ladder just to reach the ground. In the same fashion nucleons which are bound within a nucleus are in a deep potential well and we need to give the energy to them to make the potential energy zero so that they can be separated from each other.
Thus binding energy can be defined as the minimum amount of work required to completely separate a nucleus into its constituent nucleons. Binding Energy is equal to the magnitude of the negative potential energy of the nucleus and so it is always a positive number.
(If the nucleus’s potential energy is equivalent to the depth of the well you are trapped in, Binding Energy is the height of the ladder you need to escape from that well)
Now suppose you want to disintegrate the whole nucleus. That is if you want to disintegrate this nucleus, X into separate nucleons then you have to provide minimum energy to this nucleus. And that minimum energy is called the binding energy. It is typically measured in units of electronvolts (eV) or joules (J).
From Einstein’s mass-energy equivalence, the binding energy of a nucleus can be calculated as;
\begin{aligned}B(A,Z) &= \Delta mc^2\\ &= (\text{mass of individual nucleons } – \text{ mass of bound nucleus})c^2\\&=[(Z m_p + (A-Z) m_n) – M(A,Z)]c^2\\\end{aligned}
Let’s calculate the nuclear binding energy of ^4He nucleus.
\begin{aligned}\text{BE of } ^4\rm He \text{ nucleus} &=[(2m_p+2m_n)−m_{\rm He}]c^2\\&=[(2(1.00727\rm \ u)+2(1.008665\rm \ u)−4.001505\rm \ u]c^2\\&=(0.030365\rm \ u)c^2\\&=0.030365\times (931.5\rm \ MeV/c^2)\times c^2\\&= 28.28\rm \ MeV\\\end{aligned}
Thus, 28.28\rm \ MeV would be needed to fully disassemble a nucleus.
If you calculate the total binding energy of all the nuclei and plot a graph of total binding energy versus the mass number of nuclei then it will look like the graph shown below.
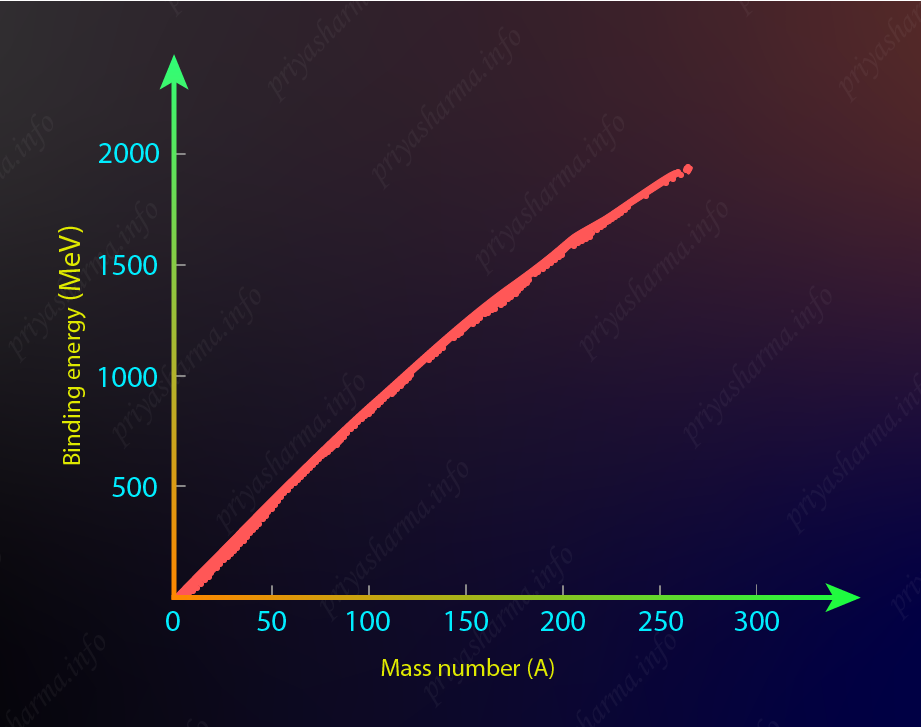
In this picture, you can see that the total binding energy linearly increases as you increase the value of A. The maximum value is about 2\rm \ GeV for the heaviest nuclei.
Now let’s calculate the average binding energy, that is, the binding energy per nucleon.
It is given by;
\begin{aligned}B_{ave.}(A,Z) &= \dfrac{\text{Total Binding Energy}}{\text{Number of Nucleons}}\\&= \dfrac{B(A,Z)}{A}\\\end{aligned}
A graph of binding energy per nucleon as a function of A is called the binding energy curve.
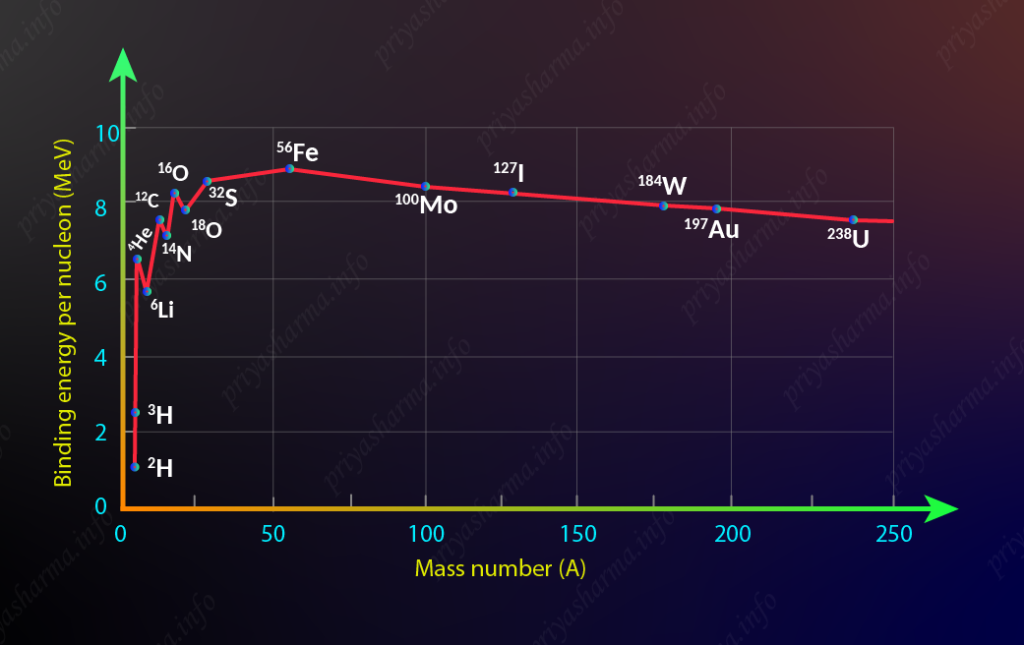
Here in this diagram, you can see that the binding energy curve increases rapidly for lighter nuclei from hydrogen up to sodium as the atomic mass increases. The reason for the rapid increase is due to the increasing nuclear force per nucleon in the nucleus, as each additional nucleon is attracted by other nearby nucleons. Binding energy per nucleon is almost saturated from magnesium to xenon and after that, there is a decrease in binding energy per nucleon as atomic mass increases. Sharp peaks for the even-even nuclei, ^4He, ^{12}C, and ^{16}O implies that they are tightly bound and more stable than the neighboring nuclei. The part of the curve to the left shows that two light elements can produce energy by fusion while the part of the curve to the right shows that a heavy element can produce energy by fission. These represent the nuclei that are most stable and the most abundant in nature. The maximum in the binding energy per nucleon occurs for ^{58}Fe. ^{58}Fe represents the most bound (lowest energy) state for nucleons.
Separation Energy:
The separation energy of a nucleus is the amount of energy required to remove one of its nucleons (proton or neutron) from the nucleus.
When talking about separation energy one should specify what is being separated from a nucleus. One can calculate 1-proton separation energy, 2-proton separation energy, 1-neutron separation energy, etc.
The 1-proton separation energy can be calculated as
\begin{aligned}S_p(A,Z) &= [M(A−1,Z−1)+m_p−M(A,Z)]c^2\\\end{aligned}
While 1-neutron separation energy can be calculated as
\begin{aligned}S_n(A,Z) &= [M(A−1,Z)+m_n−M(A,Z)]c^2\\\end{aligned}
where M(A,Z) is the nuclear mass.
The separation energy is a measure of the binding strength of the nucleon in the nucleus. Nucleons that are strongly bound in the nucleus have high separation energy, while those that are weakly bound have low separation energy. The separation energy is an important factor in nuclear reactions, such as fission and fusion, as it determines the amount of energy that is released or absorbed during these processes.
The separation energy is typically measured in units of electronvolts (eV) or megaelectronvolts (MeV).
Example 1:
Find the neutron separation energy of the nuclei ^{27}Al from the following data:
m(^{26}\rm Al)=25.986895\rm \ u
m(^{27}\rm Al)=26.981541\rm \ u
Solution
The reaction for the neutron separation from the aluminum atom is
\begin{aligned}^{27}\rm Al + E \Rightarrow ^{26}\rm Al + 1n\\\end{aligned}
We know that the separation energy can be calculated as:
\begin{aligned}E&=(m(^{26}\rm Al)+m(1n)−m(^{27}\rm Al))c^2\\&=(25.986895\rm \ u+1.008665\rm \ u−26.981541\rm \ u)c^2\\&=(0.014019\rm \ u)\times c^2\\\end{aligned}
On the other hand 1\rm \ u=931.5\rm \ MeV/c^2
So, the energy of neutron separation will be:
\begin{aligned}E&=(0.014019\ c^2)×( 931.5\rm \ MeV/c^2)\\ &=13.06\rm \ MeV\\\end{aligned}
Therefore to remove a neutron from the nucleus 13.06\rm \ MeV of energy is required. And hence this is the neutron separation energy of the nuclei ^{27}Al.
