Quantization of Angular Momentum -

Angular momentum plays an important role in classical mechanical systems as well as in quantum mechanical systems.

For a classical system, let’s take an example of our solar system. Here planets revolve around the Sun. Let’s focus on the motion of the planet, Earth. Earth is revolving around the sun and it is also rotating on its own axis while revolving. In both types of motion, the earth possesses an angular momentum. The angular momentum associated with the revolution of the earth is called orbital angular momentum while the angular momentum associated with the rotation of the earth on its own axis is known as the spin angular momentum. In the same fashion, in a quantum mechanical system, an electron revolves around the nucleus by spinning on its own axis. But unlike classical mechanics, the angular momentum is not continuous in the case of a quantum system. The electron is not necessarily allowed to have any magnitude of angular momentum. The electron faces a large number of restrictions, and due to this, it has a discrete value of angular momentum which is known as the quantization of angular momentum.

Quantization of Angular Momentum

In classical mechanics, the angular momentum of a particle is given by the cross product of its position vector ( $\vec r$ ) and its momentum vector ( $\vec P$ ) and its value is continuous.

$\begin{aligned}\vec L &= \vec r \times \vec P\\\end{aligned}$

But, in quantum mechanics, the angular momentum is quantized, which means it can only take on certain discrete values.

Why does angular momentum quantize in quantum mechanics?

Angular momentum is quantized in quantum mechanics because of the fundamental nature of quantum mechanics itself. This is because of the wave-particle duality of matter.

In quantum mechanics, particles are described by wave functions, which are mathematical functions that describe the probability of finding the particle in a particular location or state.

When a particle has angular momentum, its wave function must satisfy certain mathematical properties known as boundary conditions. These boundary conditions restrict the possible values of the angular momentum to certain discrete values.

Electron’s angular momentum

Let’s take a simple example of an electron revolving around the nucleus. Since an electron that revolves around the nucleus also spins about its own axis. So, it has two types of angular momentum, orbital angular momentum, and spin angular momentum. First, let’s discuss the orbital angular momentum of the electron.

Orbital Angular Momentum of the electron

Magnitude quantization of electron’s orbital angular momentum

After solving Schrodinger’s equation for the case of an electron in an atom, the magnitude of the orbital angular momentum of an electron is given by

$\begin{aligned}L &= \sqrt{l(l+1)}\hbar\\\end{aligned}$

Where $l$ is the azimuthal quantum number or you can say the orbital quantum number. $l$ can take on integer values from $0$ to $n-1$ , where n is the principal quantum number. Each value of $l$ corresponds to a different type of orbital with a particular shape and orientation. For example, when $l = 0$ , the orbital is an $s$ orbital, which is spherically symmetric. When $l = 1$ , the orbital is a $p$ orbital, which has two lobes oriented along the x, y, or z axes.

For s orbital ( $l = 0$ ), the total magnitude of the angular momentum would be

$\begin{aligned}L &= \sqrt{0(0+1)}\hbar\\&= 0\\\end{aligned}$

So for the case of $s$ orbital, the angular momentum of that particular electron would basically be equal to 0 units.

For $p$ orbital ( $I = 1$ ), the magnitude of the angular momentum would be

$\begin{aligned}L &= \sqrt{1(1+1)}\hbar\\&= \sqrt{2}\hbar\\\end{aligned}$

So the magnitude of the orbital angular momentum for an electron in the $p$ orbital can only have values of root $\sqrt{2}\hbar$ .

And for the case of $D$ orbital, $l = 2$ so this leads to angular moment having a magnitude of $\sqrt{6}\hbar$ .

$\begin{aligned}L &= \sqrt{2(2+1)}\hbar\\&= \sqrt{6}\hbar\\\end{aligned}$

Similarly, you can find the value of $L$ for other orbitals.

So the revolving electron can only possess certain discrete values of orbital angular momentum which is known as magnitude quantization of the orbital angular momentum which means the orbital angular moment of the electron can only have values that are allowed by a particular equation.

Space quantization of the electron’s orbital angular momentum

In addition to the quantization of the magnitude of the electron’s orbital angular momentum, there is also space quantization of the electron’s orbital angular momentum, which means that the electron’s orbital angular momentum can only be oriented along certain directions in space.

The quantization of the space component of orbital angular momentum can be expressed as:

$\begin{aligned}L_Z &= m_l \hbar\\\end{aligned}$

Here $m_l$ is the magnetic quantum number. It determines the orientation of the electron’s orbital angular momentum relative to an external magnetic field. The magnetic quantum number can take on integer values ranging from $-l$ to $+l$ , including zero. The discrete values of the magnetic quantum number determine the directions in which the electron’s orbital angular momentum can be oriented.

The combination of the quantum numbers $l$ and $m_l$ determines the specific orbital in which the electron is located. For example, an electron in an $s$ orbital has $l = 0$ and $m_l = 0$ , while an electron in a $p$ orbital has $l = 1$ and $m_l = -1$ , $0$ , or $+1$ .

To understand this a little bit better, let’s take the example of the $p$ orbital.

For $p$ orbital, $l = 1$ and $m_l = -1$ , $0$ and $1$ . Therefore we have $L_Z = -1 \hbar$ , $0$ or $+1 \hbar$ .

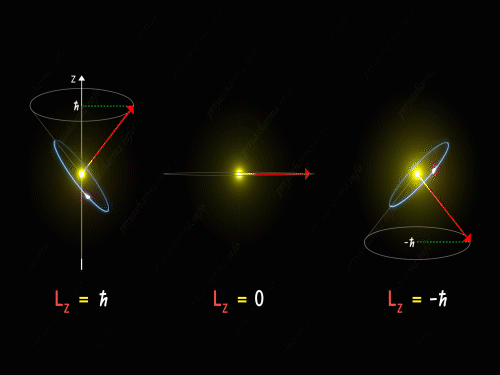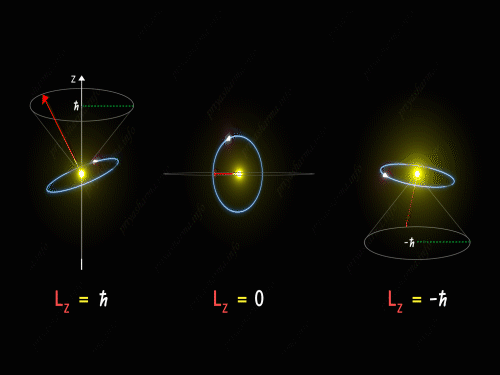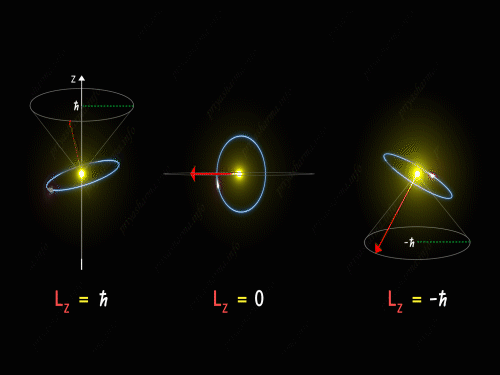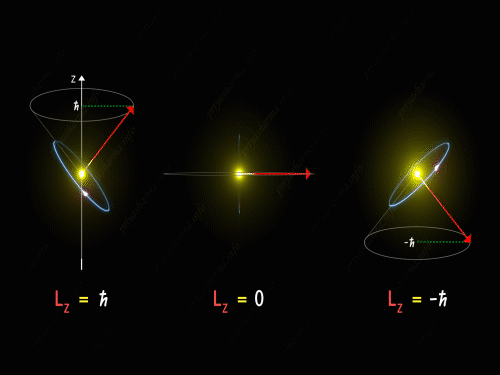
Here Z-axis is in the direction of an external magnetic field. So, for $p$ orbital, the electron’s orbit is oriented itself in such a manner that the z-component of its orbital angular momentum will have the values $-1 \hbar$ , $0$ and $+1 \hbar$ .

What does that mean?

For $L_Z = + \hbar$ the electron is revolving in a plane in such a way that the z-component of its angular momentum is always equal to $\hbar$ . Here in the above diagram, you can see the motion of the electron for different values of $m_l$ . It is known as pre seizing of the electron orbit. For $L_Z = 0$ , the orbital angular momentum is always perpendicular to the z-axis, and hence the z-component of the electron’s orbital angular momentum is always zero. And for $L_Z = – \hbar$ , the electron is orbiting in such a way that the z-component of its orbital angular momentum is always equal to $-\hbar$ .

So, the electron orbit for a $p$ orbital is restricted to three different values of the $L_Z$ that can be visualized by the different conical sections as shown in the above diagram. Thus we have seen that even the direction of the orbital angular momentum of the electron is restricted to certain precision happening around the z-axis.

The space quantization of the electron’s angular momentum has important implications for the properties of atoms and molecules, and it is essential for understanding phenomena such as the Zeeman effect, which is the splitting of spectral lines in the presence of a magnetic field.

This was all related to the orbital angular momentum but you might know that electron also has a spin angular momentum of its own. So, let’s look at that.

Spin angular momentum of the electron

Magnitude quantization of spin angular momentum

The spin angular momentum of an electron is its fundamental property. Just like in the case of orbital angular momentum, the magnitude of the spin angular momentum of an electron is given by

$\begin{aligned}S&=\sqrt{s(s+1)} \hbar\\\end{aligned}$

Here $s$ is a quantum number that has a value of $\frac{1}{2}$ . Since $s$ has only one value so the spin angular moment of the electron will also have one value and it is given by

$\begin{aligned}S&=\sqrt{\dfrac{1}{2}(\dfrac{1}{2})+1)} \hbar\\&=\dfrac{\sqrt{3}}{2} \hbar\\\end{aligned}$

Thus the magnitude of the spin angular momentum of an electron is quantized and it is always equal to $\frac{\sqrt{3}}{2} \hbar$ which is approximately equal to $5.27 \times 10^{-34}\rm \ joule-seconds$ .

So this is about the magnitude of an electron’s angular momentum. But what will be its direction?

Direction quantization of spin angular momentum

The Z-component of the spin angular momentum is given by

$\begin{aligned}S_Z&=m_s \hbar\\\end{aligned}$

Where $m_s$ is the quantum number, which is either $\frac{1}{2}$ or $-\frac{1}{2}$ . That is,

$m_s= \pm s= \pm \dfrac{1}{2}$

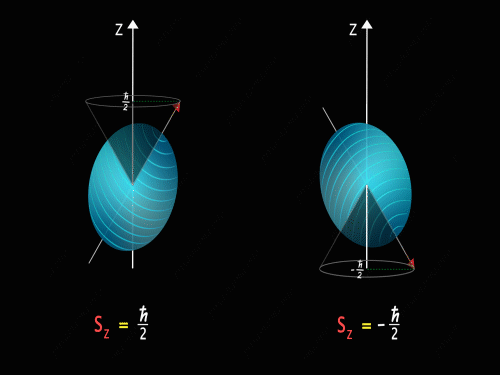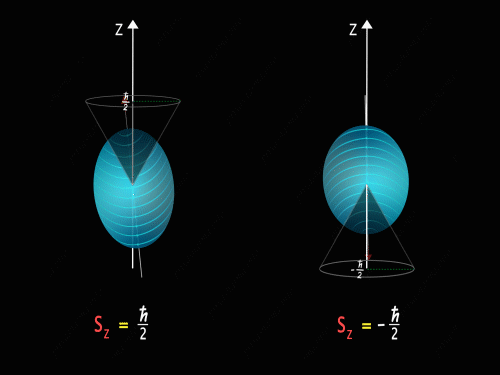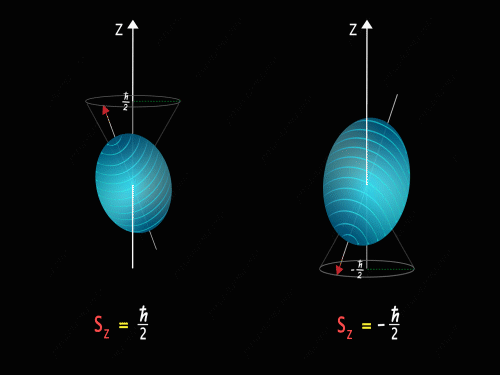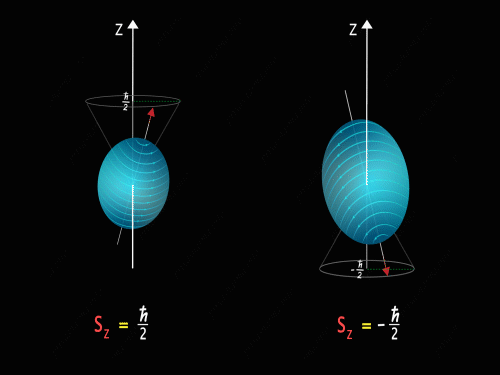
It means that the Z-component of the spin angular momentum can have values of $+\frac{\hbar}{2}$ and $-\frac{\hbar}{2}$ .

So just like in the case of orbital angular momentum here also we have some kind of precision happening around the z-axis. Here we have two kinds of precision, in the first case z-component of spin angular momentum is $+\frac{\hbar}{2}$ and in the second case, the z-component of spin angular momentum is $-\frac{\hbar}{2}$ .

Total Angular Momentum of the electron

Till now we have discussed a lot about the orbital and spin angular momentum of electrons. But what is the total angular momentum of the electron? The total angular momentum is the vector sum of orbital angular momentum and spin angular momentum. The orbital angular momentum and spin angular momentum are not necessarily conserved separately but for any kind of system, the total angular momentum is conserved.

So, the total angular momentum of an electron is given by

$\begin{aligned}\vec J &= \vec L + \vec S\\\end{aligned}$

Here $\vec L$ is the orbital angular momentum vector and $\vec S$ is the spin angular momentum vector.

The magnitude of the total angular momentum is given by

$\begin{aligned}J&=\sqrt{j(j+1)}\hbar\\\end{aligned}$

where $j$ is the quantum number associated with the total angular momentum. It takes on integer or half-integer values ranging from $|l-s|$ to $l+s$ .

For the case of $p$ orbital

$\begin{aligned}j &=1+ \dfrac{1}{2}\ \text{or}\ \left |{1-\dfrac{1}{2}} \right |\\&=\dfrac{3}{2}\ \text{or}\ \dfrac{1}{2}\\\end{aligned}$

$\begin{aligned}J&=\dfrac{\sqrt{15}}{2}\hbar\ \text{or}\ \dfrac{\sqrt{3}}{2} \hbar\\\end{aligned}$

So the revolving electron can only possess certain discrete values of total angular momentum and hence this is known as magnitude quantization of the total angular momentum.

Direction Quantization

Now just like in the orbital and spin angular momentum, the direction of the total angular momentum is also quantized which is given by the equation

$\begin{aligned}J_Z&=m_j \hbar\\\end{aligned}$

Here $m_j$ is a quantum number associated with the total angular momentum and its value is given by

$\begin{aligned}m_j &= -j,\ -(j-1),…..,\ (j-1),\ j\\\end{aligned}$

For $j = \frac{1}{2}$

$\begin{aligned}m_j &= -\dfrac{1}{2},\ +\dfrac{1}{2}\\\end{aligned}$

So,

$\begin{aligned}J_Z &= -\dfrac{1}{2}\hbar,\ +\dfrac{1}{2}\hbar\\\end{aligned}$

For $j = \frac{3}{2}$

$\begin{aligned}m_j &= -\dfrac{3}{2},\ -\dfrac{1}{2},\ +\dfrac{1}{2},\ +\dfrac{3}{2}\\\end{aligned}$

So,

$\begin{aligned}J_Z &= -\dfrac{3}{2}\hbar,\ -\dfrac{1}{2}\hbar,\ +\dfrac{1}{2}\hbar,\ +\dfrac{3}{2}\hbar \\\end{aligned}$

Thus the direction of the total angular momentum is in such a way that its Z-component will have particular values and hence this is called the space quantization of the total angular momentum.